In this paper we introduce a new approach to computing hidden features of sampled vector fields. The basic idea is to convert the vector field data to a graph structureand use tools designed for automatic, unsupervised analysis of graphs. Using a few datasets we show that the collected features of the vector fields are correlated with the dynamicsknown for analytic models which generates the data.

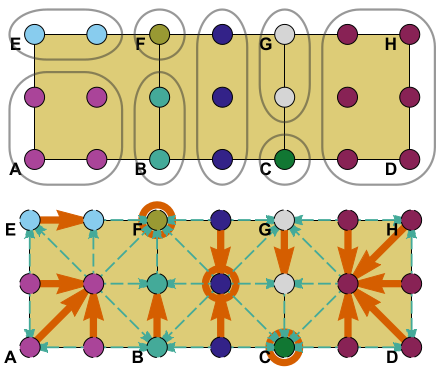
We investigate combinatorial dynamical systems on simplicial complexes considered as finite topological spaces. Such systems arise in a natural way from sampling dynamics and may be used to reconstruct some features
of the dynamics directly from the sample. We study the homological persistence of Morse decompositions of such systems as a tool for validating the reconstruction. Our approach may be viewed as a step toward applying the classical persistence theory to data collected from a dynamical system.
We present experimental results on two numerical examples.
In this paper we introduce a new approach to computing hidden features of sampled vector fields. The basic idea is to convert the vector field data to a graph structureand use tools designed for automatic, unsupervised analysis of graphs. Using a few datasets we show that the collected features of the vector fields are correlated with the dynamicsknown for analytic models which generates the data.
We plan to further develop our technology based on cooperation with industrial partners potentially interested in our data analysis methods. We are aware that our technology requires adaptation to industrial conditions.
This can only take place on the basis of long-term cooperation between science and industry.
Division of Computational Mathematics
of the Jagiellonian University
ul. prof. Stanisława Łojasiewicza 6
30-348 Kraków