Topological dynamics

Complex systems, crystal clear solutions

Analysis based on geometrical and topological approach to Big Data

What we do

We develop data analysis technologies based on well-established branches of mathematics: dynamics and topology. The methods are complementary to the statistical approach and give new, geometric insights into qualitative properties of the data.

We designed our core technology to describe the cloud of vectors, i.e. sampled vector fields. Such data appears, in particular, in:

  • simulations of dynamical systems;
  • optical methods of flow visualization in fluids (see PIV – Particle Image Velocimetry);
  • velocity/magnetic fields analysis.
LEARN HOW

Partners we work with

Become our partner

Publications

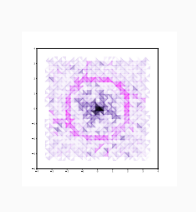
Unsupervised Features Learning for Sampled Vector Fields
18.08.2020
Unsupervised Features Learning for Sampled Vector Fields
Juda, M., 2019. arXiv:1911.10023 [cs, math].
Download pdf
Persistent Homology of Morse Decompositions in Combinatorial Dynamics
18.08.2020
Persistent Homology of Morse Decompositions in Combinatorial Dynamics
Dey, T., Juda, M., Kapela, T., Kubica, J., Lipiński, M., Mrozek, M., 2019. Persistent Homology of Morse Decompositions in Combinatorial Dynamics. SIAM J. Appl. Dyn. Syst. 18, 510–530. https://doi.org/10.1137/18M1198946
Download pdf
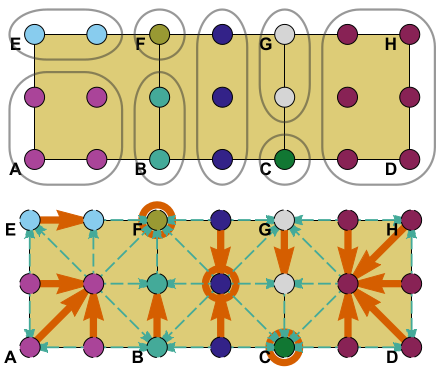
Conley–Morse–Forman Theory for Combinatorial Multivector Fields on Lefschetz Complexes
18.08.2020
Conley–Morse–Forman Theory for Combinatorial Multivector Fields on Lefschetz Complexes
Mrozek, M. Conley–Morse–Forman Theory for Combinatorial Multivector Fields on Lefschetz Complexes . Found Comput Math 17, 1585–1633 (2017). https://doi.org/10.1007/s10208-016-9330-z
Download pdf
Browse publications

Contact us

We plan to further develop our technology based on cooperation with industrial partners potentially interested in our data analysis methods. We are aware that our technology requires adaptation to industrial conditions.

This can only take place on the basis of long-term cooperation between science and industry.

Phone
Email
mateusz.juda@ii.uj.edu.pl

Visit us

Division of Computational Mathematics
of the Jagiellonian University

ul. prof. Stanisława Łojasiewicza 6
30-348 Kraków